Contents

On-demand webinar
How Good is My Shield? An Introduction to Transfer Impedance and Shielding Effectiveness
by Karen Burnham
PCB designers have a difficult task when it comes to routing a circuit board. Things get a lot more complicated when the design involves high-speed signals.
To help these designers, we have drafted a list of the best high-speed PCB routing practices that will assist them in achieving that perfect high-speed design.
Consider these PCB routing dos and don’ts to achieve controlled impedance in your design.
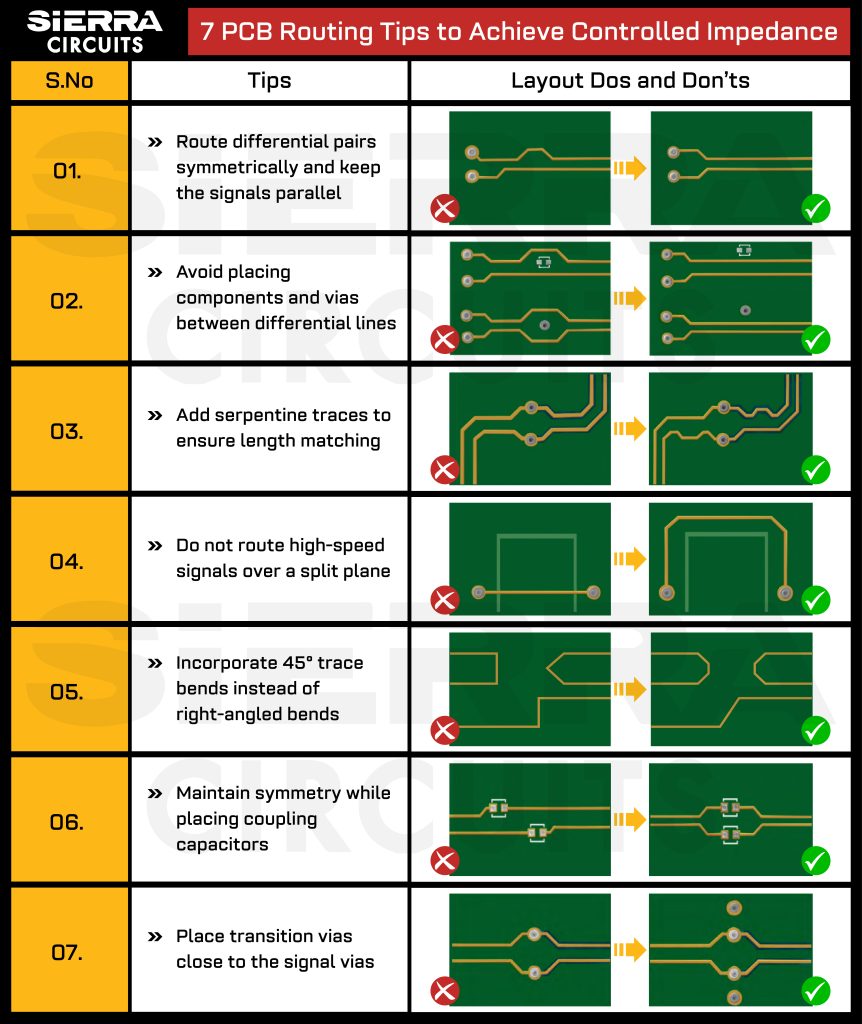
1. Route high-speed signals over a solid ground plane
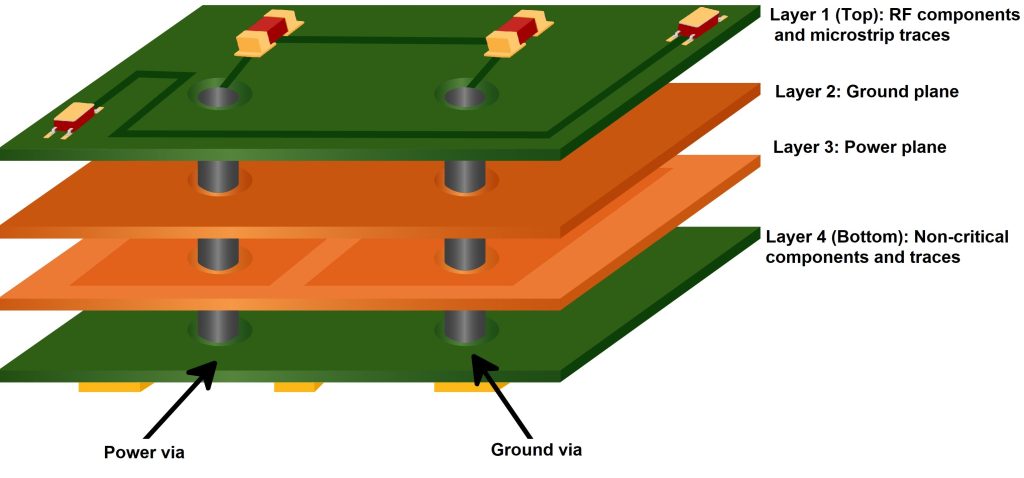
As a rule of thumb, having a common ground plane below signal traces is most beneficial. For best results, a designer should incorporate at least a four-layer PCB. A four-layer PCB allows devoting one of the inner layers to a full ground plane.
A ground plane is a sheet of copper, forming one of the layers of the PCB and covering the entire area of one of the layers of the PCB. This ensures minimal impedance between any two ground points in the PCB. This ground plane should never be broken by routing any tracks in it.
When the external layer nearest to the ground plane is used to mount all the high-speed components, like RF components, using microstrip traces or coplanar traces. The opposite side is used for mounting less critical components. The second inner layer is used for power planes. The power planes are made as large as possible to reduce the impedance.
A double-sided PCB may be the right choice when it comes to cost minimization. Achieving this is quite difficult. When there is a requirement to route tracks on both sides of the PCB in the same area, then a good ground plane is no longer guaranteed.
The only solution is then to implement ground planes on both sides of the traces that are interconnected by plenty of vias, as shown in the image below.
In the article, The Darker Side – RF and high-speed PCBs: How to avoid basic mistakes”, Circuit Cellar 253, Robert Lacoste says, “Designing a double-sided PCB becomes complex when the ground plane gets shared between the top and bottom layers.
The designer should ensure that there is at least a full ground plane under the most critical section. The top side must be used for routing as much as possible with a few traces on the bottom side.
Lots of interconnecting vias are needed to interconnect the top and the bottom grounds. Most importantly, traces should never cross the high-speed traces on the opposite side in a two-layer board.
Robert states that having isolated ground planes for the logic and analog components interconnected at a single point can reduce the noise through the ground planes. However, it is quite challenging to accurately implement such an idea as it is mandatory to route all the traces going from one region to the other exclusively above this interconnecting point (as shown in the image below).
If this is not followed it gives a very good antenna that will either transmit or receive spurious signals. He recommends a full single ground for better results than split grounds, as long as the placement of the components is adequate.
Usually, a split ground plane is avoided, unless there is a specific need like reducing strong ESD risks and reducing analog ground noise.

High-Speed PCB Design Guide
8 Chapters - 115 Pages - 150 Minute ReadWhat's Inside:
- Explanations of signal integrity issues
- Understanding transmission lines and controlled impedance
- Selection process of high-speed PCB materials
- High-speed layout guidelines
Download Now
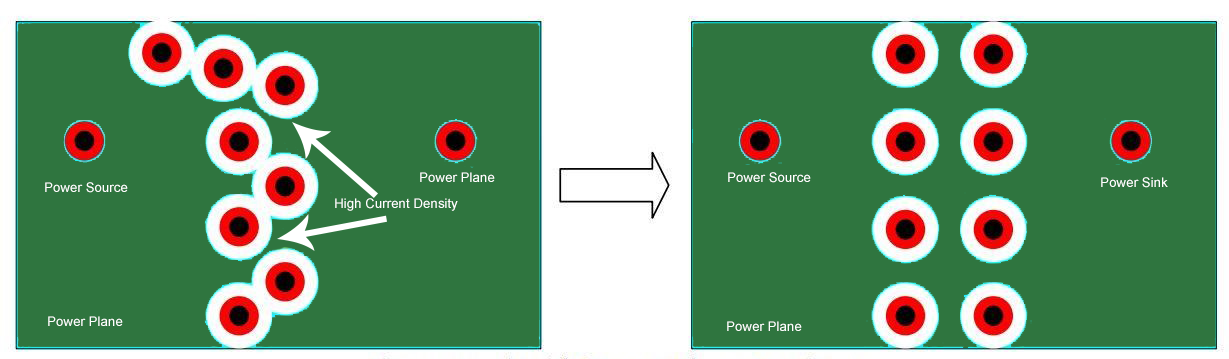
2. Avoid hot spots by placing vias in a grid.
The signal vias produce voids in the power and ground planes. Improper positioning of vias can create plane areas in which the current density is increased. These regions are called hot spots.
These hot spots must be avoided. The best solution is to place the vias as shown in Figure (4) in a grid that leaves enough space between the vias for the power plane to pass. As a thumb rule, place vias 15 mils apart wherever possible.
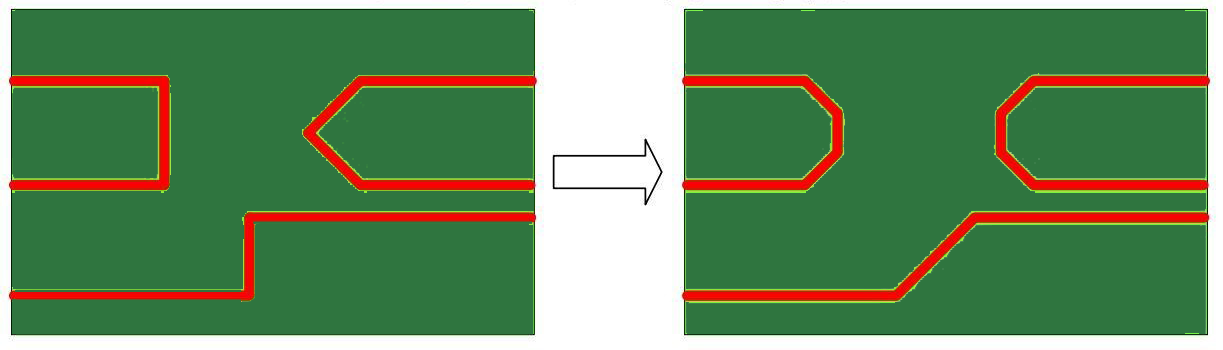
3. Keep 135⁰ trace bends instead of 90⁰ while routing high-speed signals.
The bends should be kept minimum while routing high-speed signals. If the bends are required, then 135° bends should be implemented instead of 90°as shown in Figure (5, Right side). At 90 degrees, smooth PCB etching is not guaranteed. Also, very high-speed sharp edges act as an antenna.
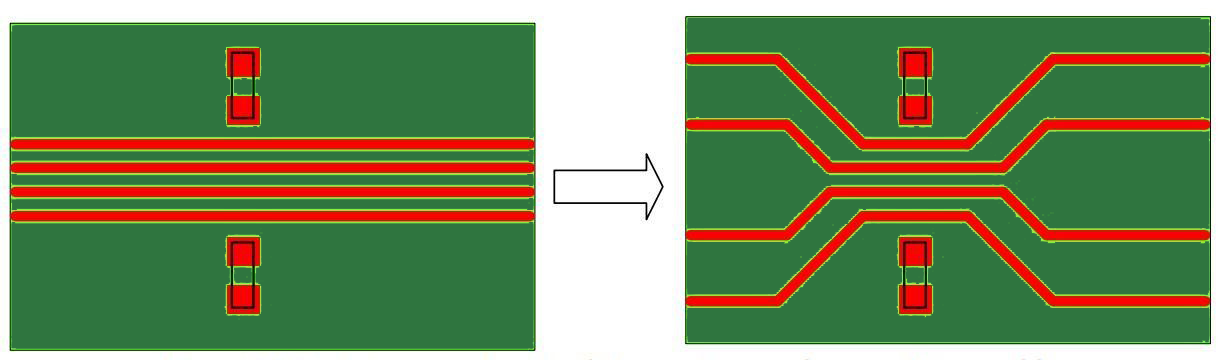
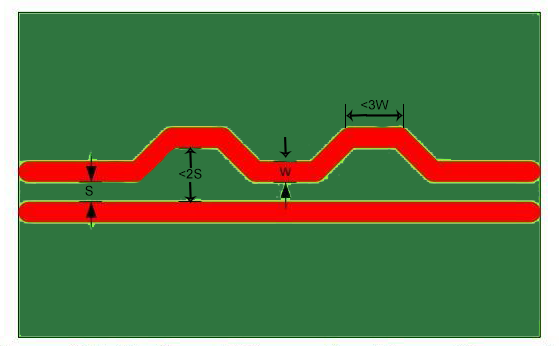
To achieve a specific trace length, serpentine traces are needed as shown in figure (6). A minimum distance of 4 times the trace width must be maintained between adjacent copper in the same trace.
Each segment of the bends should be 1.5 times the trace width. Most of the DRCs in CAD tools do not check these minimum distances, as the traces are part of the same net.

4. Increase the distance between the signals outside the bottleneck regions to evade crosstalk.
A minimum distance should be maintained between traces to minimize the crosstalk. The crosstalk level depends on the length and the distance between the two traces. In some areas, the routing of traces reaches a bottleneck where the traces are closer than desired.
In such situations, the distance between the signals outside the bottleneck should be increased. Even if the minimum requirement is met, the spacing can be increased a little further.
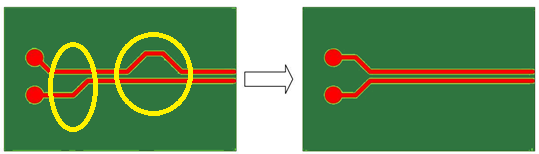
5. Avoid long stub traces by implementing daisy chain routing to maintain signal integrity
The long stub traces may act as antennas and consequently increase problems complying with EMC standards. Stub traces can also create reflections that negatively affect signal integrity. Pull-up or pull-down resistors on high-speed signals are common sources of stubs. If such resistors are required then route the signals as a daisy chain as shown in Figure (8).

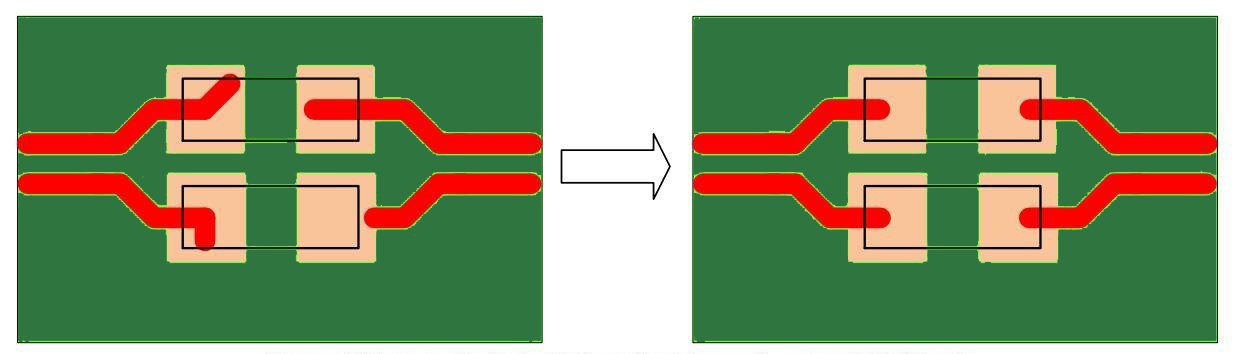
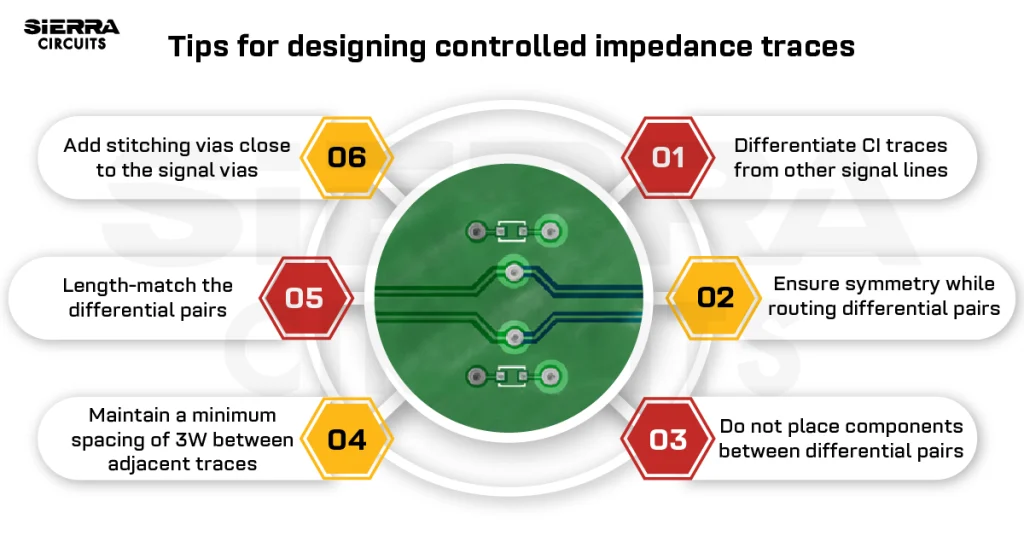
6. Do not place any components or vias between differential pairs
When routing high-speed differential pairs parallel to each other, a constant distance should be maintained between them. This distance helps to achieve the specified differential impedance. The designer should minimize the area in which the specified spacing is enlarged due to pad entries. The differential pairs should be routed symmetrically.
The designer should not place any components or vias between differential pairs even if the signals are routed symmetrically as shown in Figure (10). The placement of components and vias between differential pairs could lead to EMC problems and impedance discontinuities.
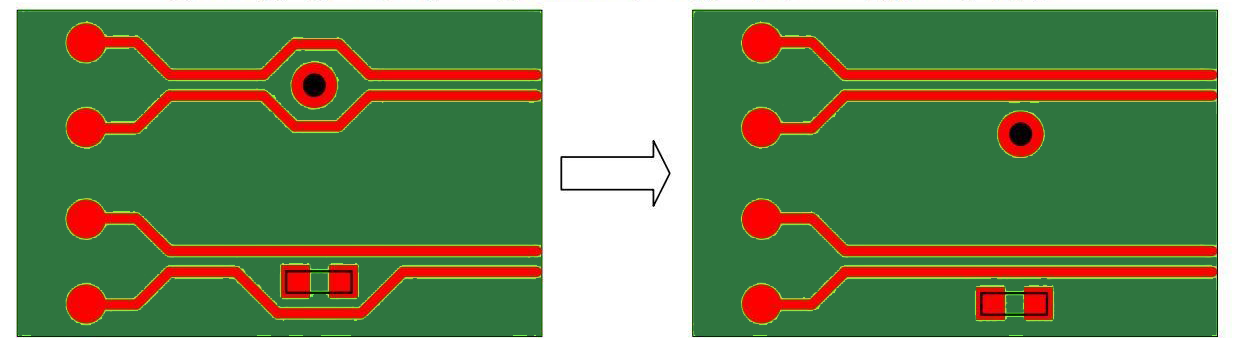
Some high-speed differential pairs need serial coupling capacitors. These capacitors should be placed symmetrically. The capacitors and the pads produce impedance discontinuities. Capacitor sizes such as 0402 are preferable over 0603. Larger packages such as 0805 or C-packs must be avoided. Read how can we reduce parasitic capacitance in PCB layout.

Since the vias introduce an enormous discontinuity in impedance, the number of vias must be reduced and should be placed symmetrically.

While routing a differential pair, both the traces should be routed on the same layer so that the impedance requirements are met as shown in Figure (13). Also, the same number of vias should be included in the traces.
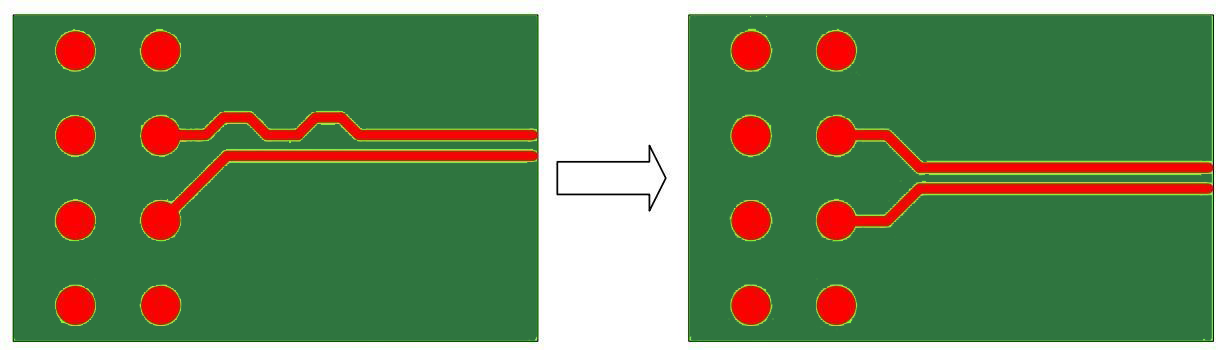
7. Incorporate length matching to achieve a tight delay skew between positive and negative signals.
The high-speed interfaces have additional requirements concerning the time of arrival at a destination known as clock skew between different traces and pairs of signals. For instance, in a high-speed parallel bus, all data signals need to arrive within a time period in order to meet the setup and hold time requirements of the receiver.
The PCB designer should ensure that such permitted skew is not exceeded. To achieve this requirement, the length matching is necessary. Read our post on propagation delay concerning signals in a PCB.
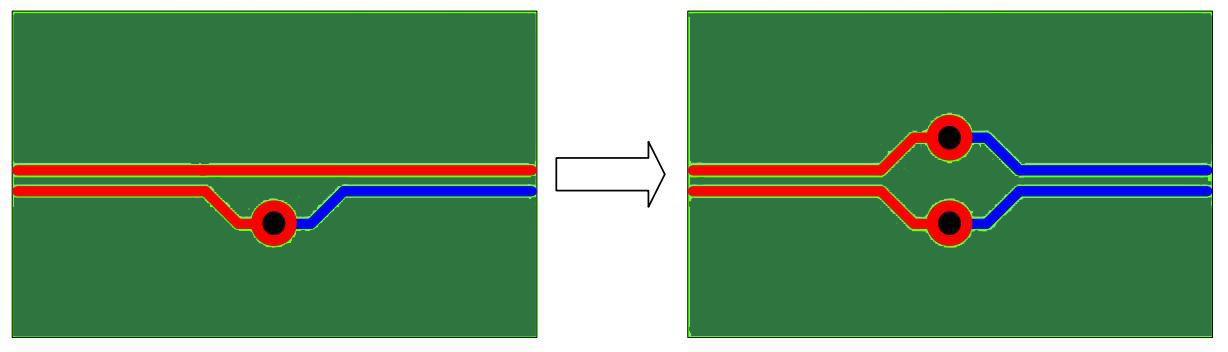
The differential pair signals demand a very tight delay skew between the positive and negative signal traces. Hence, any length differences should be compensated by using serpentines. The geometry of serpentine traces should be carefully designed as shown in Figure (14) to reduce impedance discontinuity.
The designer should place the serpentine traces at the root of the length mismatch. This ensures that the positive and negative signal components are propagated synchronously over the connection as shown in figure (15).
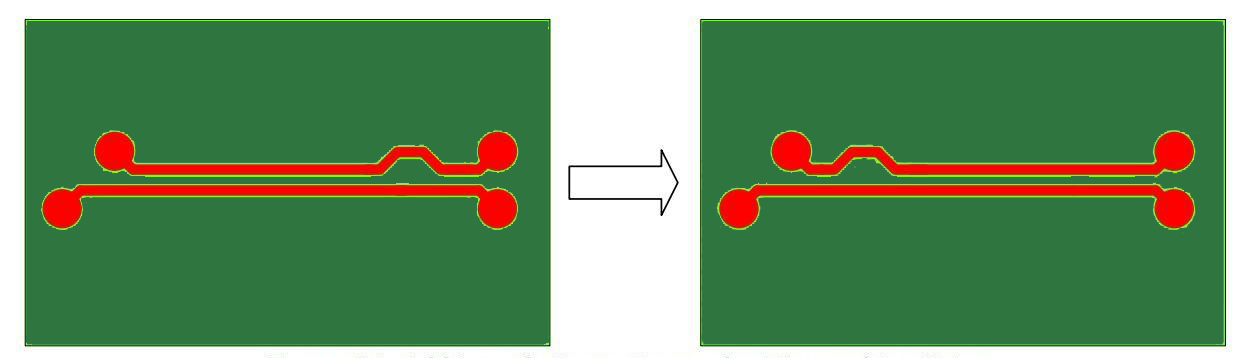
The bends are usually the source of length mismatches. The compensation should be planted very close to the bend with a maximum distance of 15mm as shown in the below figure (16).
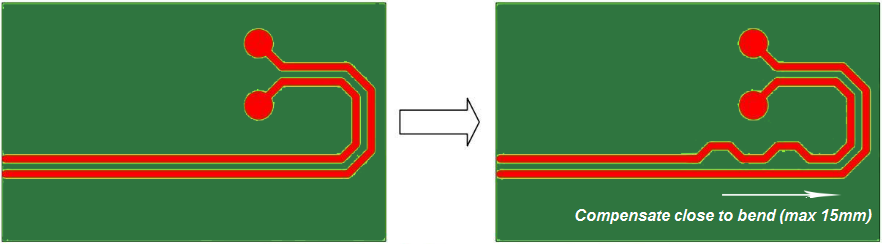
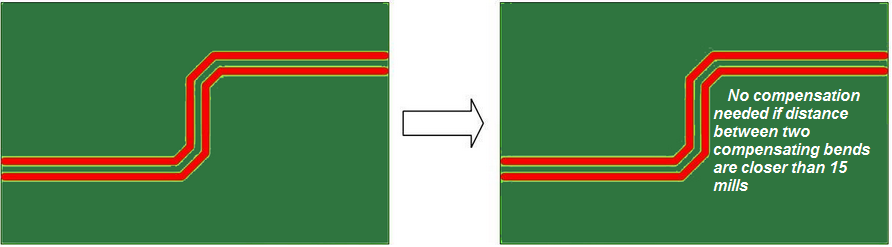
Generally, two bends compensate for each other. If the bends are closer than 15mm then no additional compensation with serpentines is necessary. The signals should not traverse asynchronously over a distance of more than 15mm.
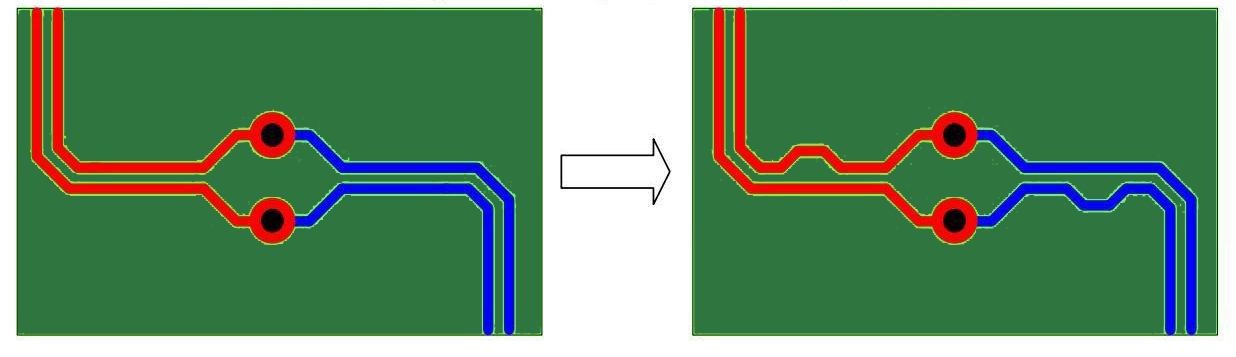
The mismatches in each segment of a differential pair connection should be matched individually. In figure (18) shown below, the vias separate the differential pair into two segments. The bends need to be compensated individually here. This ensures that the positive and negative signals are propagated synchronously through the vias. The DRC overlooks this violation since it only checks the length difference over the whole connection.
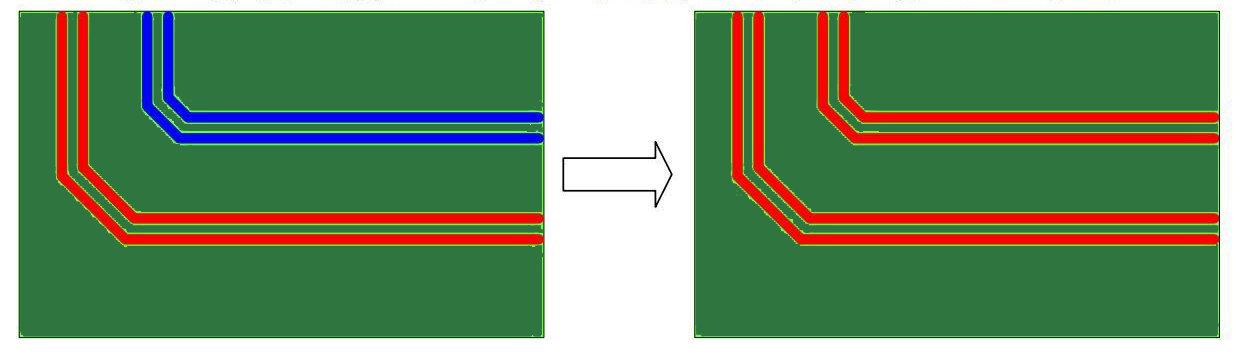
The signal speed is not the same in all the layers of a PCB. Since it is hard to figure out the difference, it is preferable to route signals on the same layer if they need to be matched.
Some CAD tools also consider the trace length inside a pad as its total length. The figure shown below depicts two layouts that are similar from an electrical point of view.
In Figure (20) on the left, the traces inside the capacitor pads do not have an equal length. Even though the signals do not use internal traces, some CAD tools consider this as part of the length calculation and display a length difference between the positive and negative signals. In order to minimize this, ensure that the pad entry is equal for both signals.
In the same way, some CAD tools do not consider the length of vias when calculating the total length. Since differential pairs should have the same amount of vias in both traces, the error does not affect the length matching. However, it can affect calculations for matching two differential pairs or the matching of parallel buses.
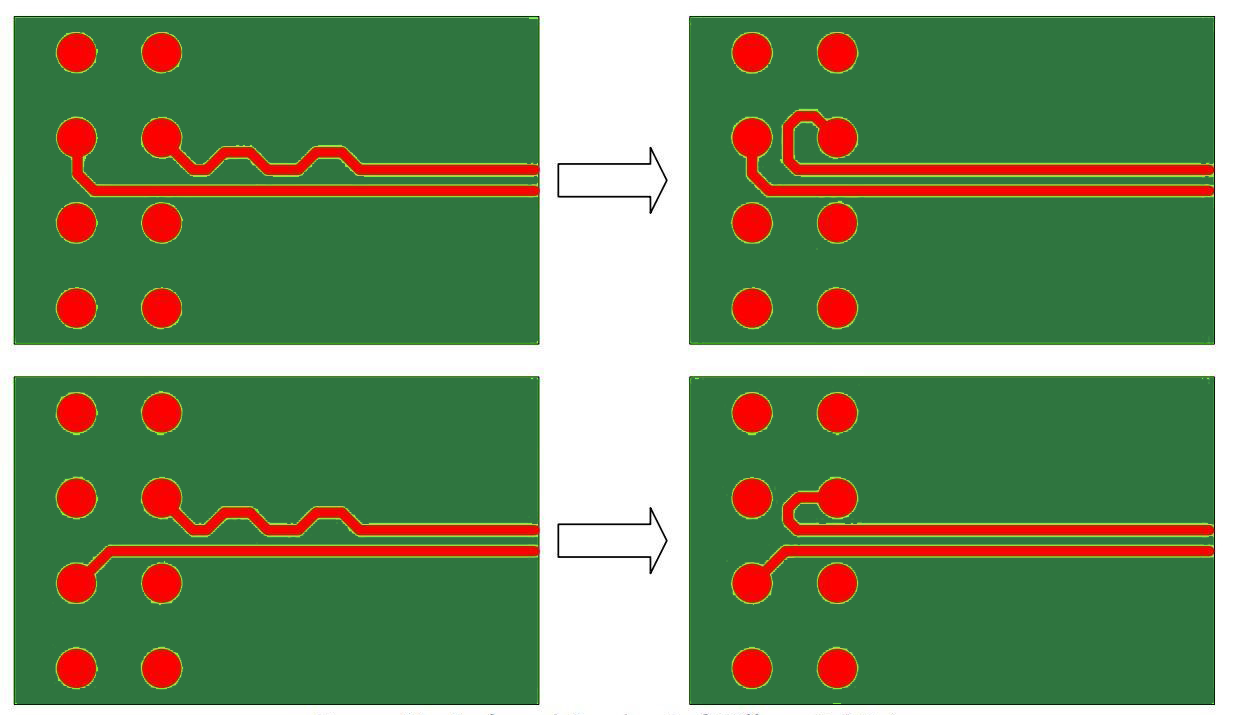
Symmetric breakout of differential pair signal is preferred as shown in figure (21), wherever possible in order to avoid the serpentine traces.
Small loops can be included for the shorter trace instead of serpentine traces if there is enough space between pads. This is generally preferred over a serpentine trace.
To get some valuable insights into overcoming routing issues in high-density circuit boards, read 5 HDI PCB routing challenges with solutions.
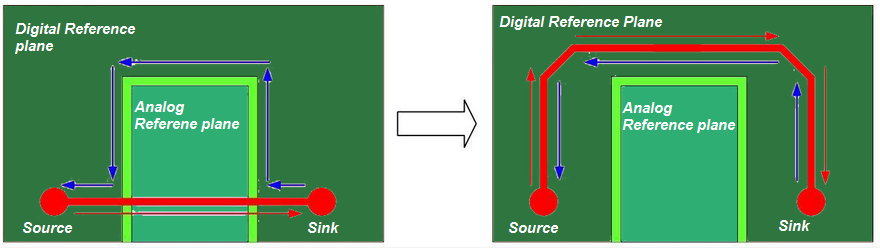
8. Do not route signal over a split plane
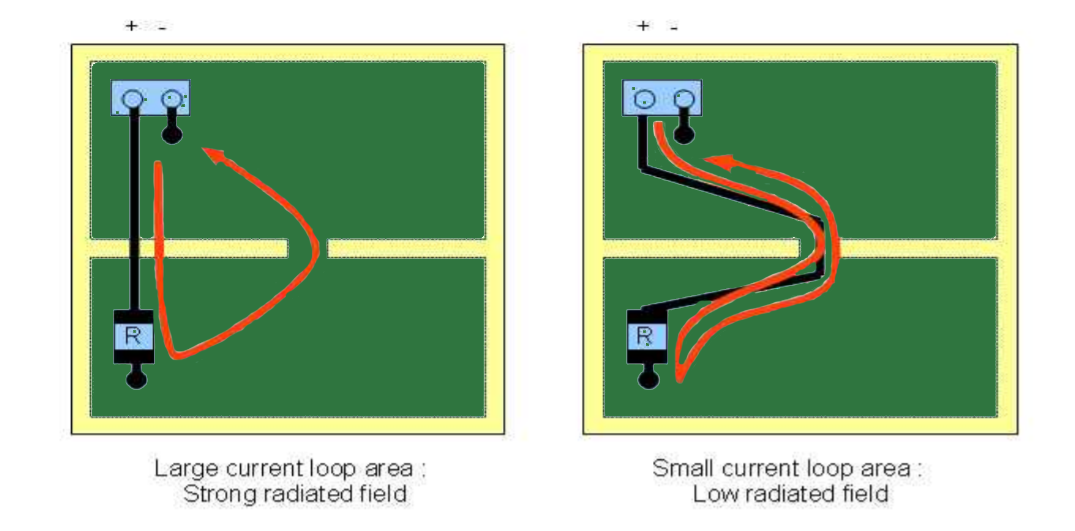
An incorrect signal return path results in noise coupling and EMI issues. The designer should always think of the signal return path when routing a signal. The power rails and low-speed signals take the shortest return current path as shown in figure (23). In contrast to this, the return current of high-speed signals tries to follow the signal path.
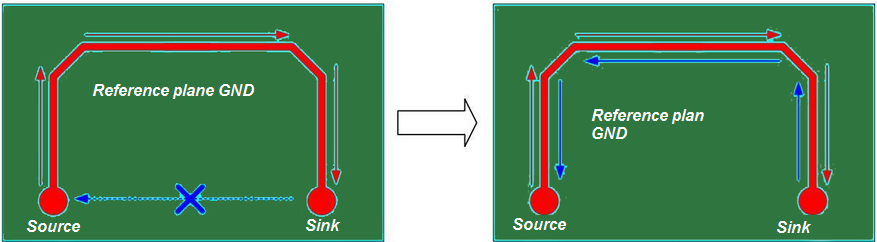
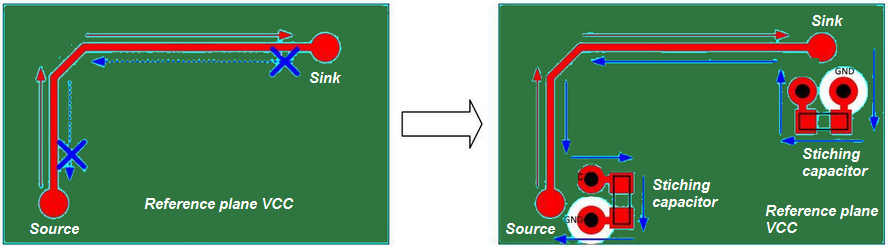
A signal should not be routed over a split plane as the return path is not able to follow the signal trace. Refer Figure (24). If a plane is split between a sink and source, route the signal trace around it. If the forward and return paths of a signal are separated, the area between them acts as a loop antenna.
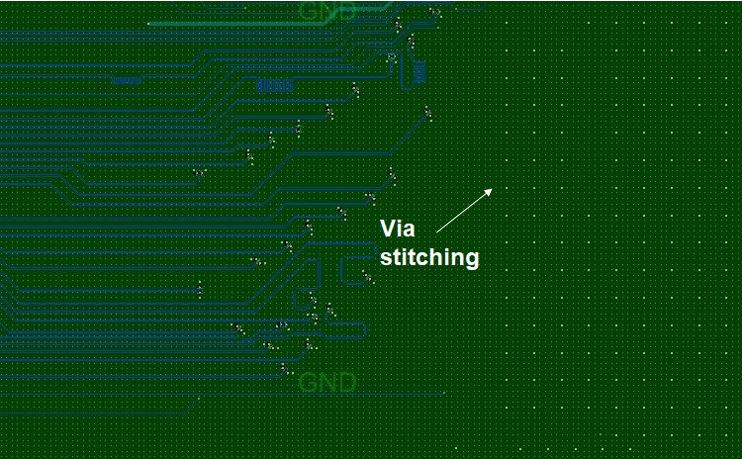
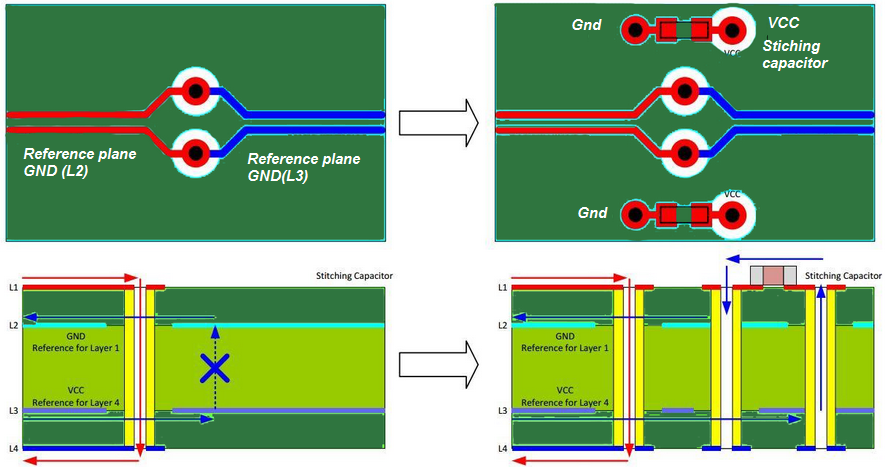
Stitching capacitors should be incorporated if a signal needs to be routed over two different reference planes. The stitching capacitor enables the return current to travel from one reference plane to the other. The capacitor should be placed close to the signal path so that the distance between the forward and return path is kept small. Generally, the values of stitching capacitors are between 10nF and 100nF.
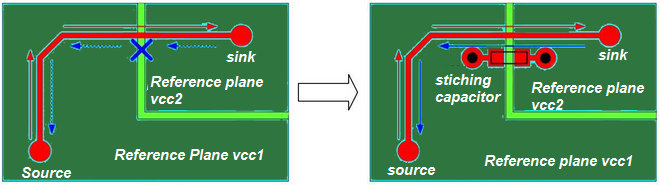
In general, plane obstructions and plane slots must be avoided. If it is really necessary to route over such obstruction then stitching capacitors should be used as shown in Figure (25).
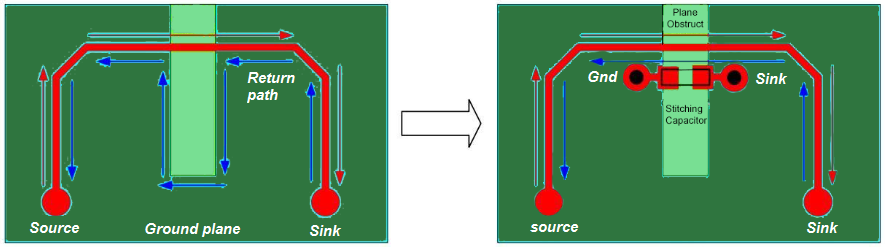
The designer should look out for voids (no copper area) in reference planes while routing high-speed signals. Voids in reference planes are generated when placing vias close together as shown in Figure (25). Large void areas should be avoided by ensuring adequate separation between vias. It is better to place fewer ground and power vias in order to reduce via voids.
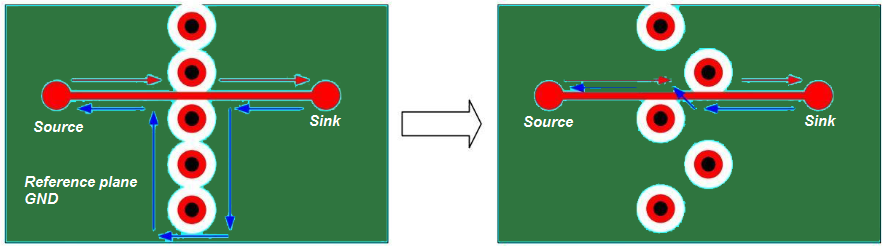
The return path should be considered at the source and sink of a signal. In Figure (27) shown below, the left design is considered to be a bad design. Since there is only one single ground via on the source side, the return current cannot travel back over the reference ground plane as intended. The return path is the ground connection present on the top layer instead.
The problem at hand is that the impedance of the signal trace is calculated as referenced to the ground plane and not to the ground trace on the top layer. Hence, it is essential to place ground vias at the source and sink side of the signal. This allows the return current to travel back on the ground plane as shown in figure (27) on the right.
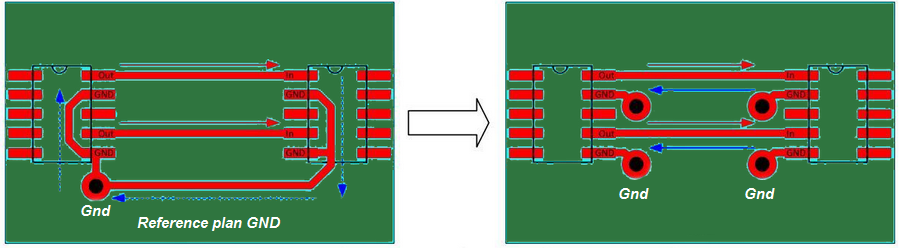
When a power plane is considered as a reference to a signal, then the signal should be able to propagate back over the power plane. The signals are referenced to the ground in the source and sink.
To switch the reference to the power plane, stitching capacitors should be incorporated at the sink and source. If the sink and source are utilizing the same power rail for their supply, then the bypass capacitors can act as stitching capacitors if they are placed close to the signal start/exit point as shown in Figure (28).
The ideal value for the stitching capacitor is between 10nF and 100nF.
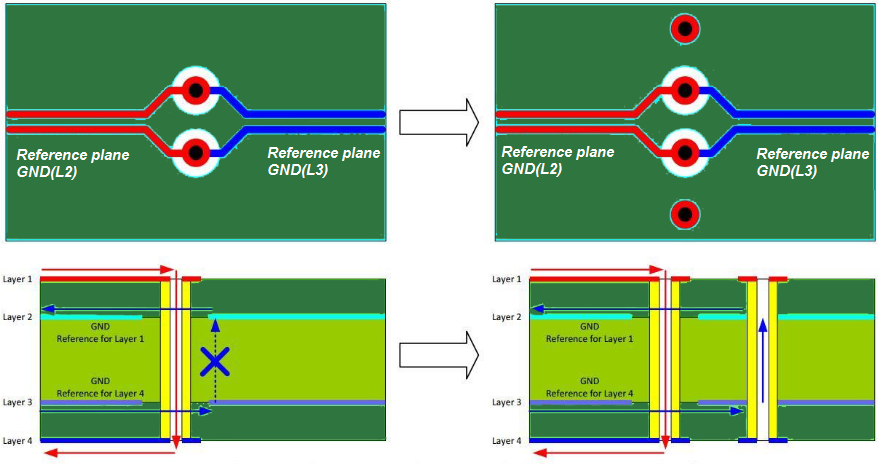
When a differential signal switches a layer, the reference ground plane will also be switched. Hence, stitching vias should be added close to the layer change vias as shown in Figure (29) on the right. This permits the return current to change the ground plane. When dealing with differential signals, the switching ground vias should be placed symmetrically.
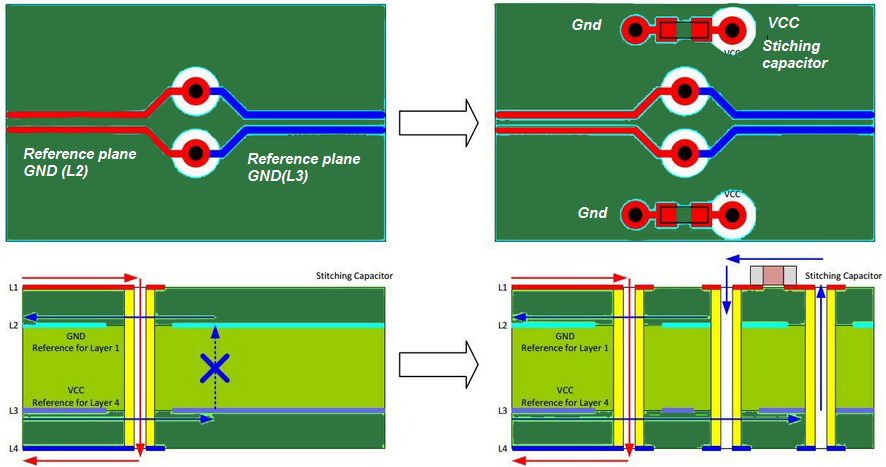
When a signal switches to a different layer that has a different reference plane then stitching capacitors should be implemented.
This permits the return current to flow from the ground to the power plane through the stitching capacitor as shown in figure 30 on the right. Also, the stitching capacitor placement and routing should be symmetrical when differential pairs are considered.
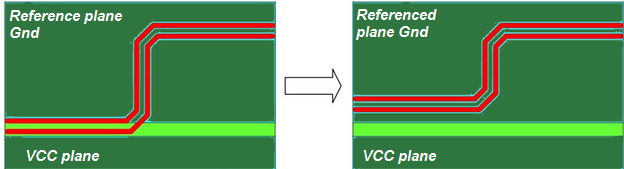
The designer should not route high-speed signals on the edge of the reference planes or close to PCB borders. This can have an adverse impact on the trace impedance.
9. Separate analog and digital ground planes to reduce noise
Defining separate Analog and Digital ground sections approach makes it easy in the schematic to determine which components and pins should be connected to the digital ground and which ones to the analog ground section.
These designs can be routed by placing two different ground planes as reference. The two planes should be placed accurately. The digital and analog components should be placed underneath the respective sections, as shown in Figure (32, right).
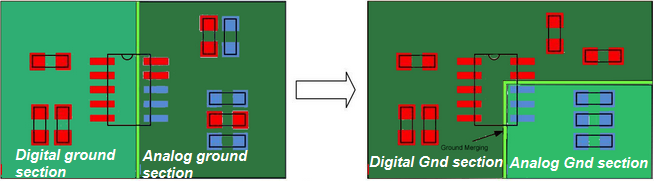
In a mixed-signal design with split planes, the digital signal should not be routed over an analog ground plane and the analog signal should not be routed over the digital ground plane.
10. Split the layouts virtually between analog and digital grounds.
In the virtual split approach, the analog and digital ground are not separated in the schematic diagram. Also, the two ground domains are not electrically separated in the layout either.
Interestingly, the layout is split virtually, i.e., an imaginary separation is drawn between the analog and digital ground. The components should be placed carefully considering the correct side of the virtually split planes.
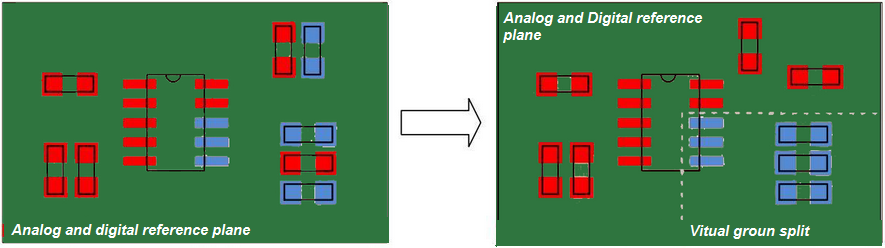
The designer should keep in mind the virtual line between the two ground domains during the high-speed PCB routing process.
Neither the digital nor the analog signal trace is allowed to cross the virtual split line. The virtual split line should not have a complicated shape since there is no plane obstruction to keep the analog and digital return current separated.
Learn How To Breakout a .5mm BGA
11. Choose a component width close to the track width
Let’s understand our last high-speed PCB routing tip. The board design begins with the schematic, specifically with the selection of the components. Surface-mount devices (SMD) are preferred since smaller components and shorter wires result in more stable high-speed performances.
Robert Lacoste, R&D consultant and Trainer at ALCIOM says choosing the package can get tricky sometimes. One beneficial criterion is to look at the track width calculated for a 50-ohm impedance.
The best high-speed performances are usually accomplished if the component’s width is close to the track width. This will lower the impedance matching issues between the track and the component pad.
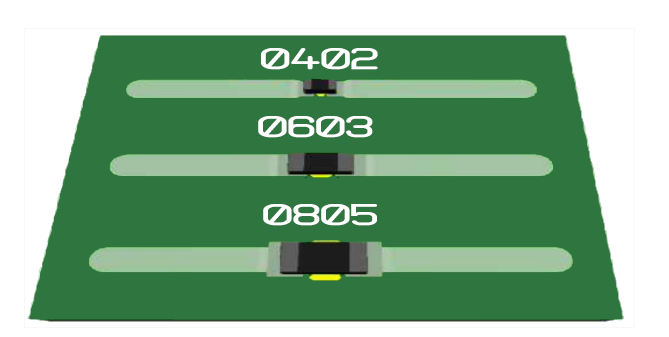
The impedance mismatches can be reduced by selecting those components that have a package that is almost the same size as the calculated track width. The test points should be planned at the schematic phase.
All the above-mentioned high-speed PCB routing practices can help a designer craft a board that not only results in an efficient design but also a manufacturing-friendly one. To find out the other important factors starting from BOM to final QC read, mastering the art of PCB design basics.






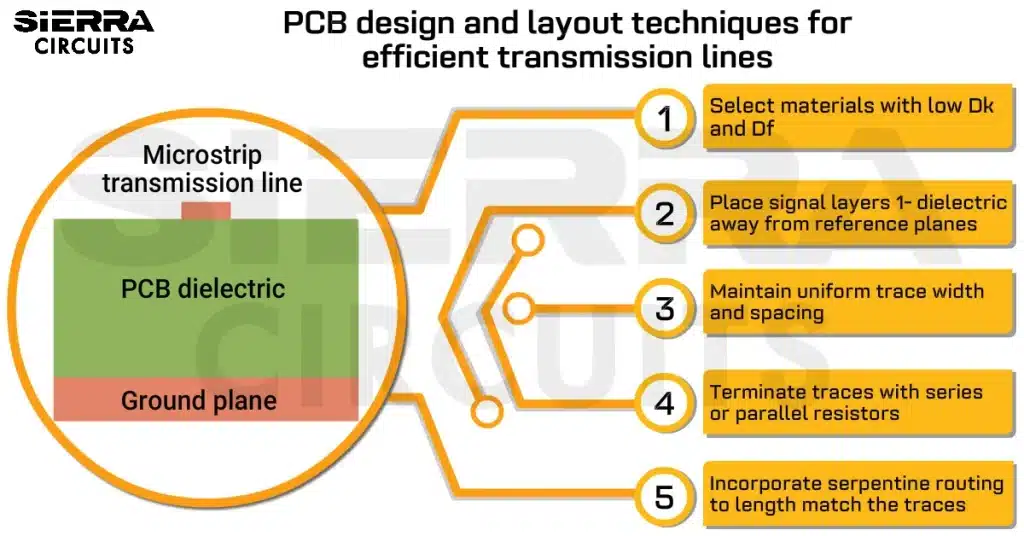
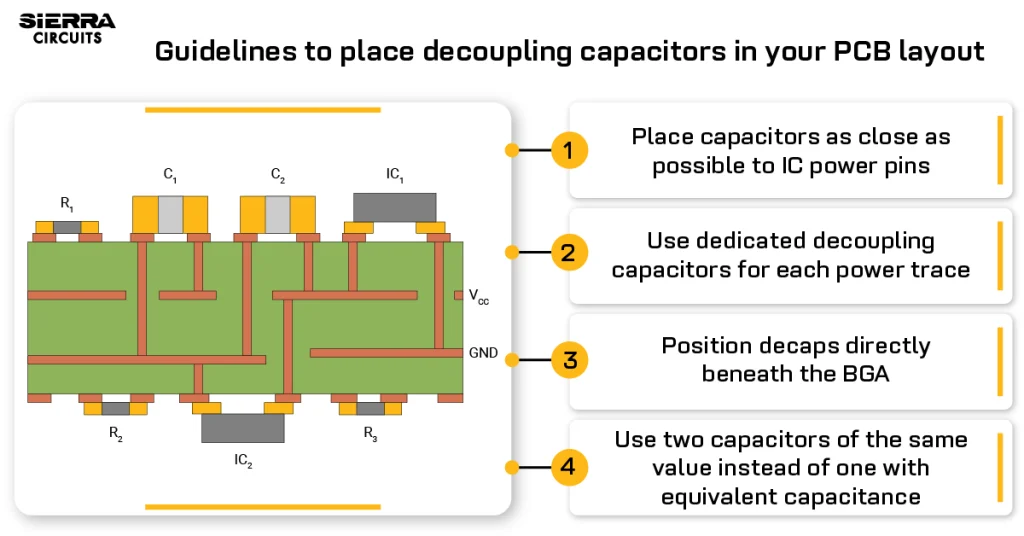
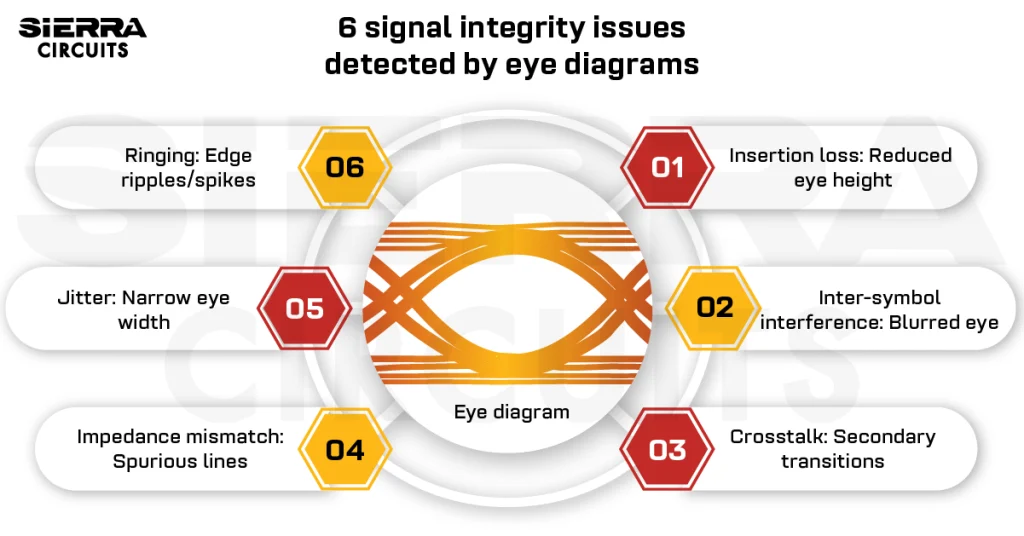




I’m currently working on a high-speed PCB design and have some questions about transmission line effects. From my understanding, when we talk about “transmission line” effects, we refer to issues like crosstalk, reflections, and ringing. These effects don’t usually appear at low frequencies where the PCB trace behaves more like an ideal transmission medium, similar to how we expect a wire to behave based on early school lessons.
I also understand that the 50-ohm value isn’t related to the line resistance, which is typically very small and less than 1 ohm. Instead, this value comes from the ratio of the inductance (L) and capacitance (C) on the line. Adjusting the trace height above the ground plane (affecting C) or changing the trace width (affecting L) can change the impedance of the line.
Since the reactance of L and C depends on the signal frequency, I have a few questions:
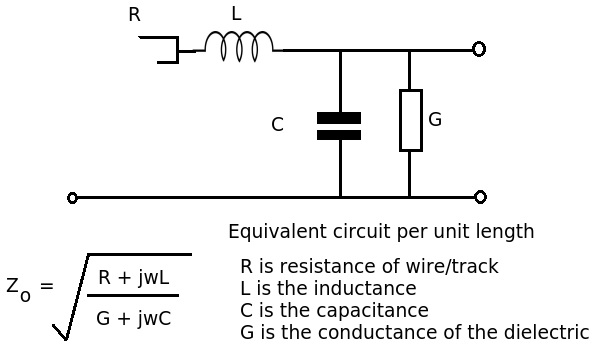
First, let’s have a look at the formula and equivalent circuit for a transmission line:
1. Impedance vs. Reactance
Reactance describes the opposition to changes in current or voltage for individual components like inductors and capacitors. A transmission line, however, incorporates resistance (R), inductance (L), and capacitance (C), making impedance the appropriate term. Impedance is defined as the ratio of the voltage phasor to the current phasor in a transmission line, encompassing all these elements.
2. Why 50Ω?
The 50Ω impedance arises from the ratio of inductance to capacitance per unit length of the transmission line. When R is much less than jωL and G is close to zero, these values become negligible, simplifying the expression to the square root of L/C, making it frequency-independent.
3. Deviating from Standard Impedance
Technically, you can choose any impedance, such as 100Ω or 167Ω, but it’s generally advisable to stick to standard values like 50Ω. This is because finding compatible components, such as connectors for non-standard impedances, can be challenging. Additionally, there are extensive resources and guidelines available for designing transmission lines on PCBs. As a side note, the impedance of free space is 376.73031… ohms, which is an interesting fundamental constant of our universe.
4. When Actual Resistance Matters
At low frequencies, the resistance (R) of the transmission line may become significant as the inductive reactance (jωL) is small. At very high frequencies, dielectric losses can also become a concern, affecting the performance of the transmission line.
A transmission line inherently possesses distributed inductance and capacitance throughout its length, which can be conceptualized as countless small inductors and capacitors arrayed along the line, as shown below:

Each inductor slows down the rate at which its corresponding capacitor can charge. As we continue to subdivide the transmission line into smaller and smaller segments, the inductors and capacitors become proportionately smaller as well. But does this subdivision affect the line’s behavior? Not really. We can slice the transmission line into any number of segments—from just a few to an infinite number—making the inductors and capacitors arbitrarily small in the process.
The critical insight here is that the absolute values of these inductors and capacitors are not what dictate the line’s properties. What truly matters is the ratio of inductance to capacitance, a value that remains constant regardless of how much we divide the line. Since the characteristic impedance of the transmission line is determined by this ratio, it remains unchanged whether the line is divided into more segments or made longer. This consistency is key to understanding why the fundamental behavior of the transmission line doesn’t shift as we alter its segmentation or length.
Building on what Myrtle mentioned:
Consider a long chain of inductors and capacitors, all starting with 0 Volts and Amps. When you introduce a voltage step at one end, the inductors slow down the charging of the capacitors, causing a steady current to flow. This current is proportional to the voltage you applied. By dividing the voltage by the current, you can determine the resistance that this infinite transmission line mimics. In an ideal infinite transmission line, it behaves just like a resistor from the outside.
However, this behavior only holds if the voltage step can continue to propagate down the line. Here’s the key insight: if you have a short transmission line but add a resistor matching the characteristic impedance across its end, the line will appear infinite from the perspective of the source. This technique is known as terminating the transmission line.
Bernd has provided an excellent overview. I’d like to expand on a couple of points:
2) The 50 Ohms Impedance: While 50 Ohms is considered a standard value, it’s worth noting that the dielectric constant of the material does exhibit slight frequency dependence. This means that the impedance you calculate for a trace at 1 GHz will differ slightly at 10 GHz. However, this variation is usually small and only becomes a concern in very high-frequency designs. If you’re working one high-speed PCB design, you’re likely already aware of the nuances involved.
4) Impact of Resistance on PCB Traces: For typical PCB designs using FR4, dielectric losses start to become significant around 0.5 to 1 GHz. However, resistance is a critical factor when dealing with high-current lines. For instance, a 6 mil wide trace of 1 oz copper carrying 1 Amp over a 1-inch length will have approximately 0.1 Ohms of resistance. This translates to a 0.1V voltage drop and a temperature rise of around 60°C. If such a voltage drop is unacceptable for your design, you’ll need to either widen the trace or use thicker copper.
As a general guideline, if your trace lengths are under 1 inch, DC resistances can often be considered negligible.
The reason why the effective impedance of an ideal transmission line remains constant can be explained in a straightforward way. When we refer to a “transmission line,” we’re talking about wires that are considered “long” relative to the wavelength of the electromagnetic wave traveling through them. “Long” here means that the physical length of the line is greater than the wavelength of the signal being transmitted. This concept becomes particularly significant at high frequencies or over long distances. The relationship between the wavelength of a signal and the length of a trace is crucial.
As has been noted, every trace on a PCB has a certain inductance and capacitance per unit length. These values are typically expressed as L (inductance per unit length) and C (capacitance per unit length). The total inductance and capacitance of a segment of the transmission line would then be the product of these per-unit values and the segment’s length (i.e., L_total = L * length and C_total = C * length).
Now, think about a sine wave traveling along this transmission line. In the context of a dielectric or air medium, electromagnetic waves propagate at nearly the speed of light (around 150 ps per inch). At any given moment, a specific portion of the sine wave interacts with a segment of the trace equivalent to its wavelength. Lower frequency waves have longer wavelengths, meaning they interact with a longer segment of the trace, thus encountering greater inductance and capacitance. Conversely, higher frequency waves have shorter wavelengths and interact with shorter segments of the trace, encountering lesser inductance and capacitance.
The key point here is that both the effective inductance (L) and capacitance (C) that a wave “sees” are proportional to the wavelength of the signal. Since the characteristic impedance of a transmission line is given by Z0=√(L∕C), the proportional relationship between L and C with respect to wavelength cancels out. As a result, waves of different frequencies perceive the same effective impedance Z0.