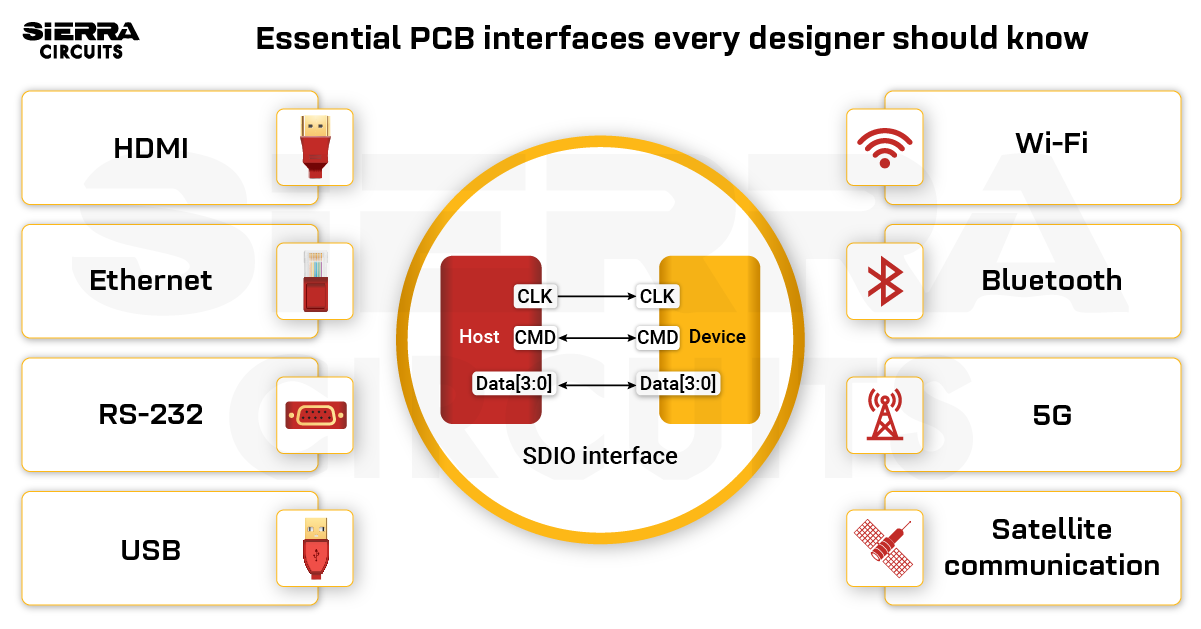
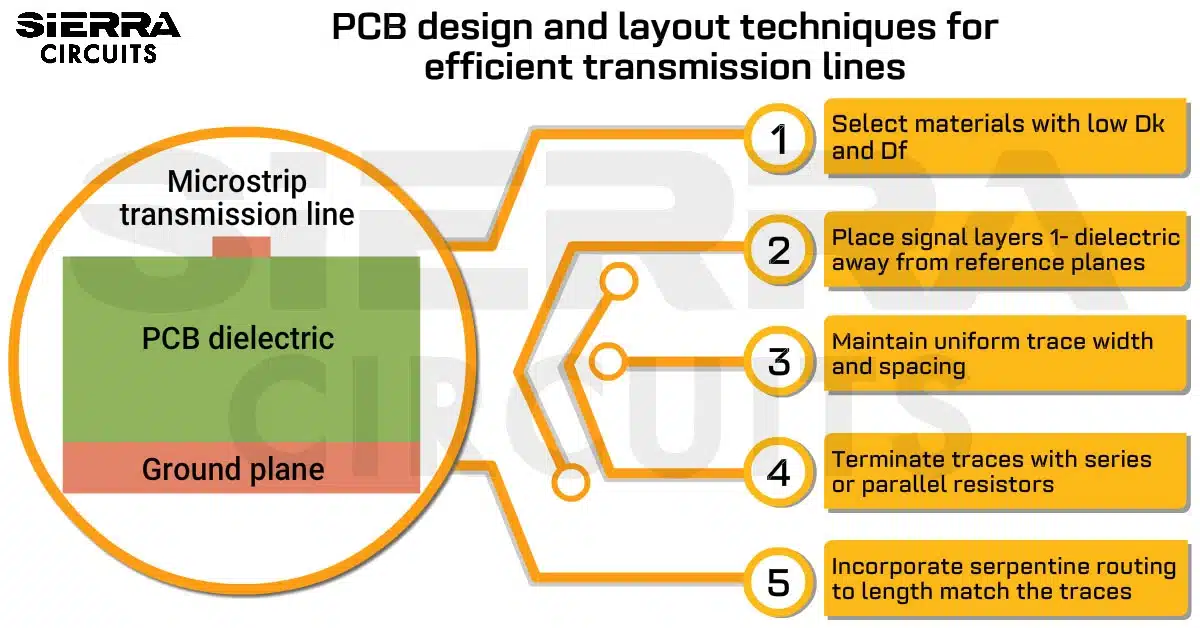
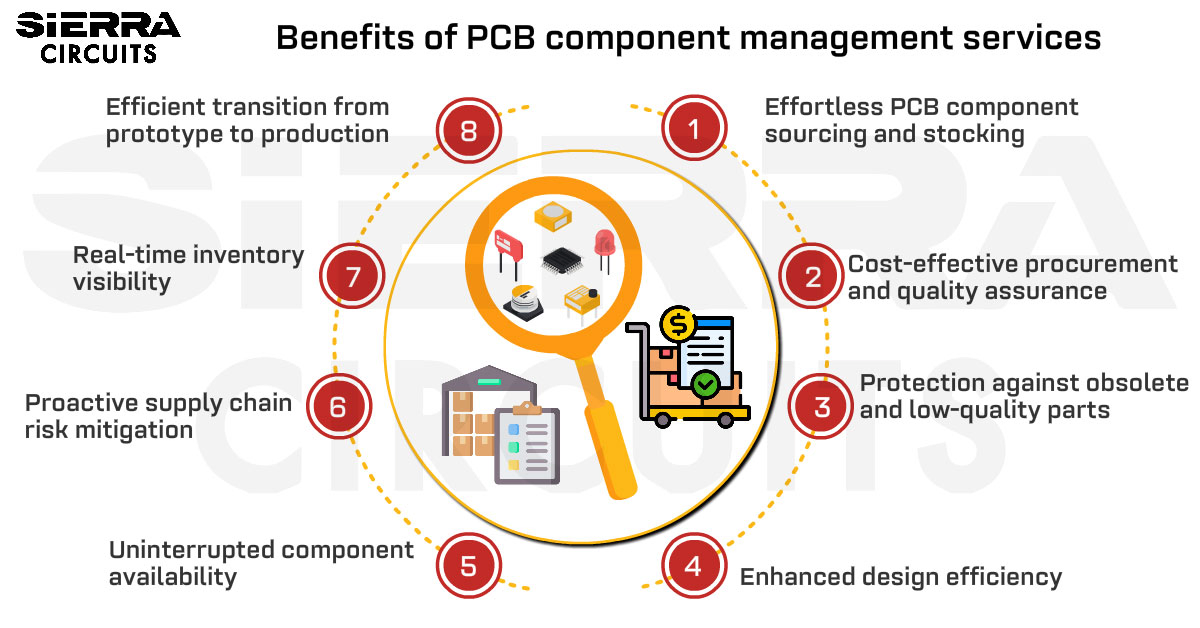
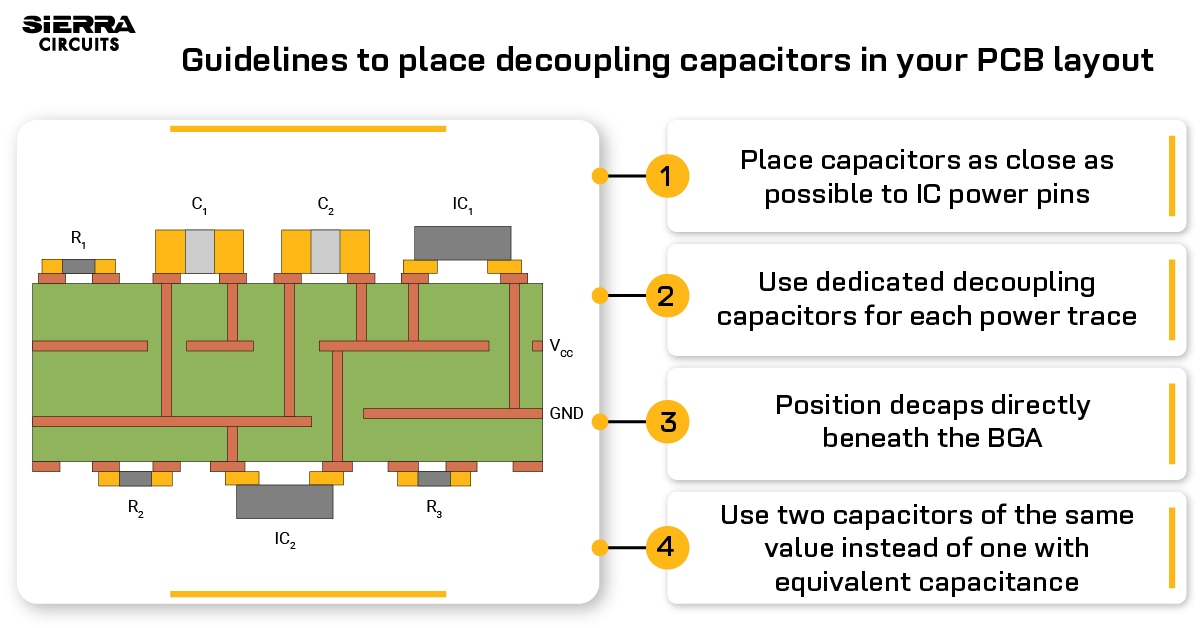
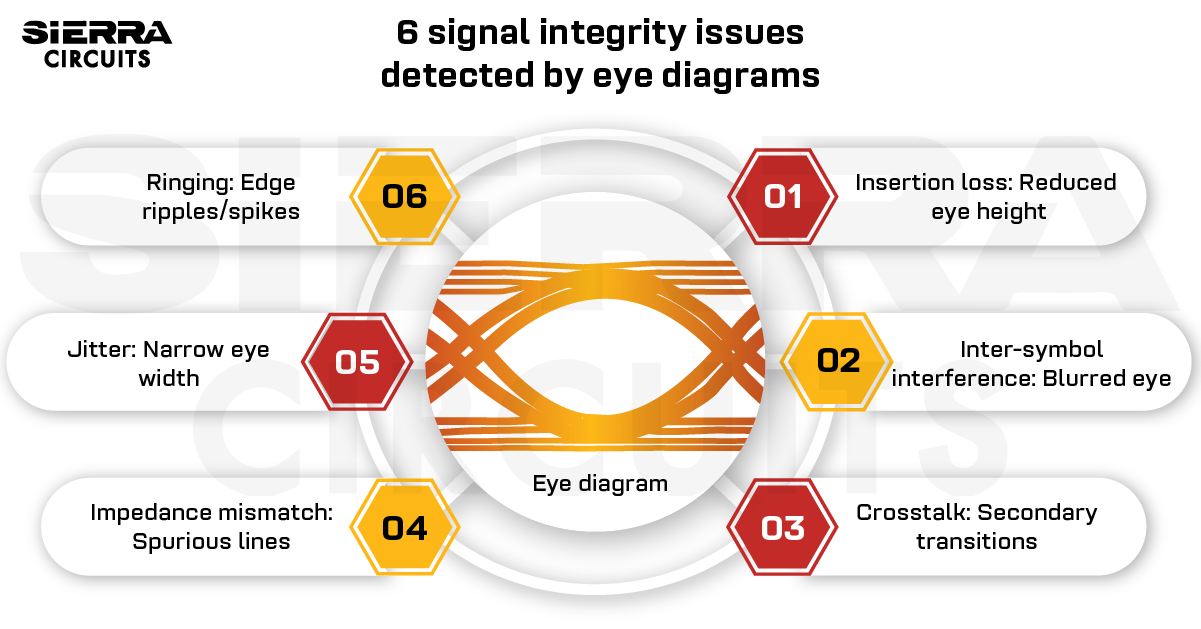
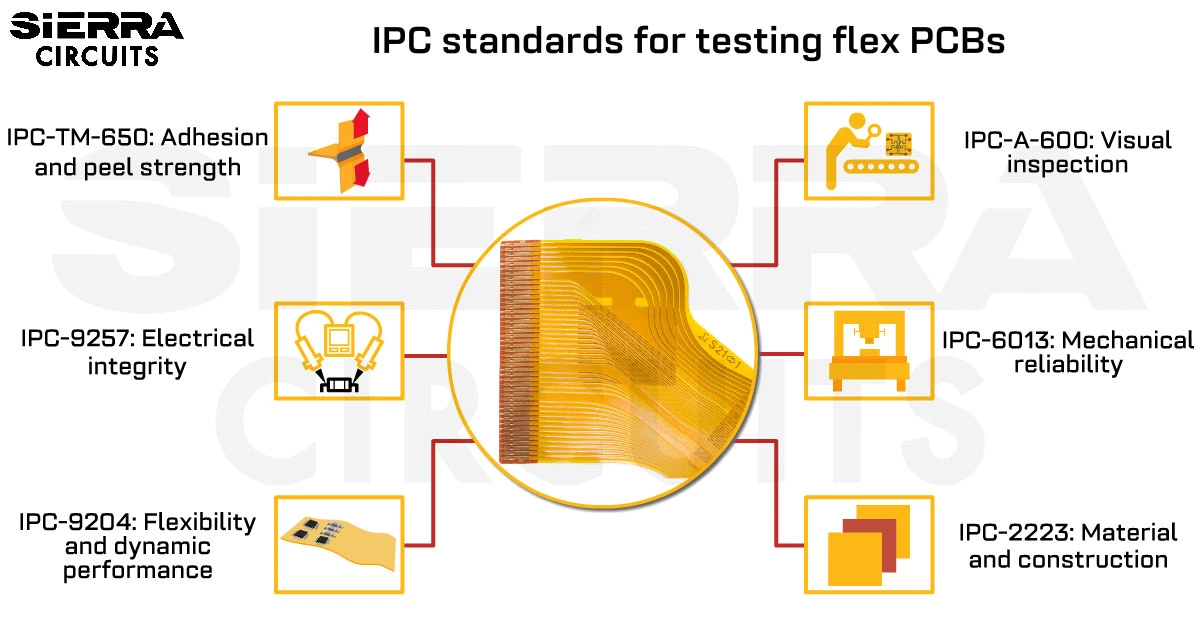
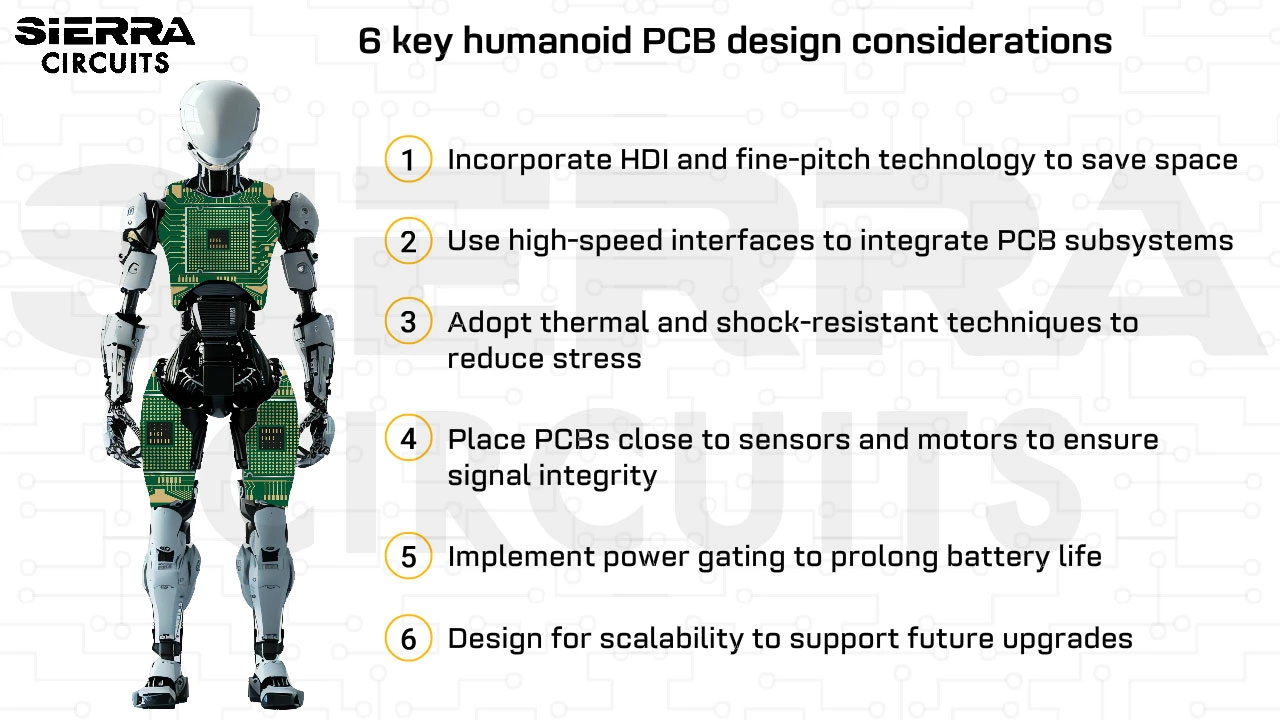
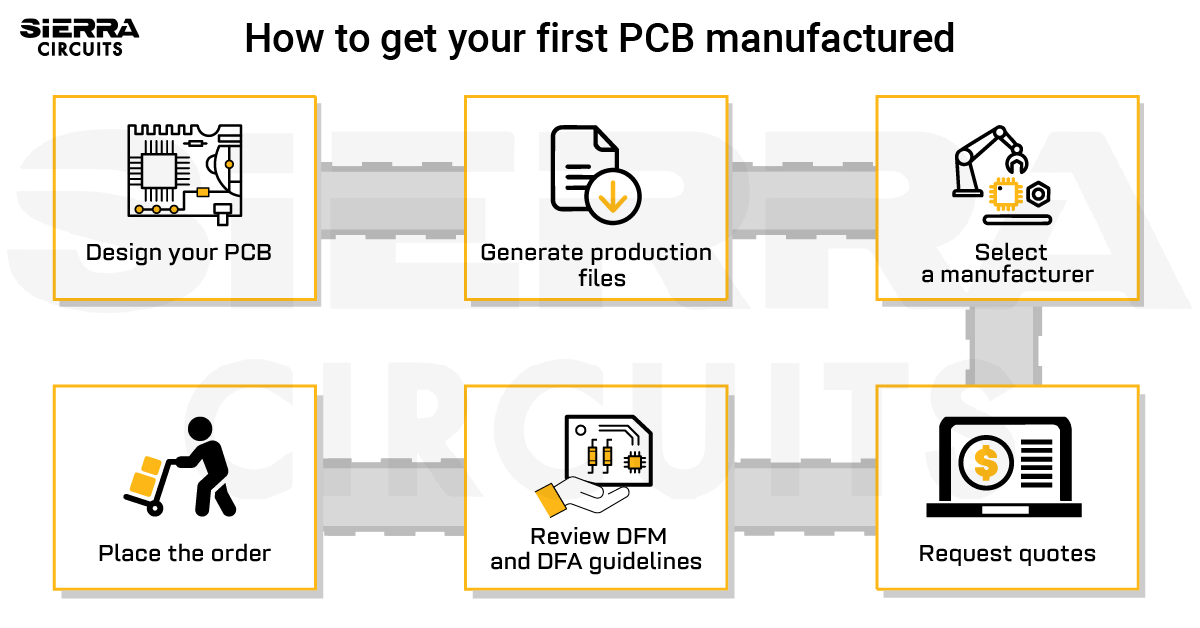
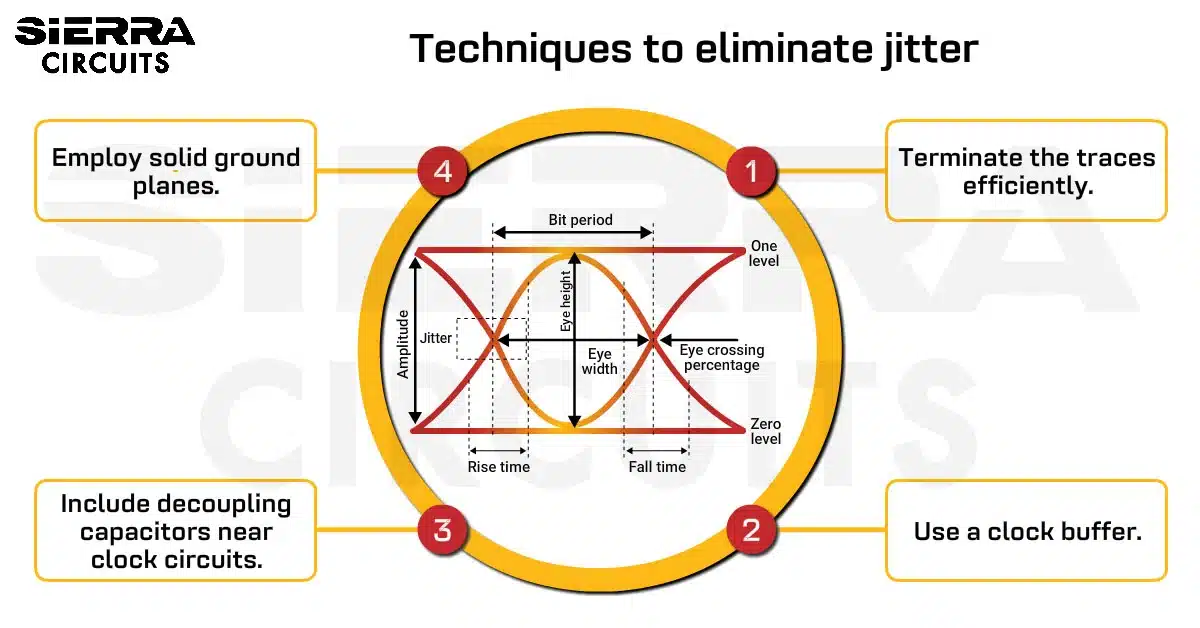
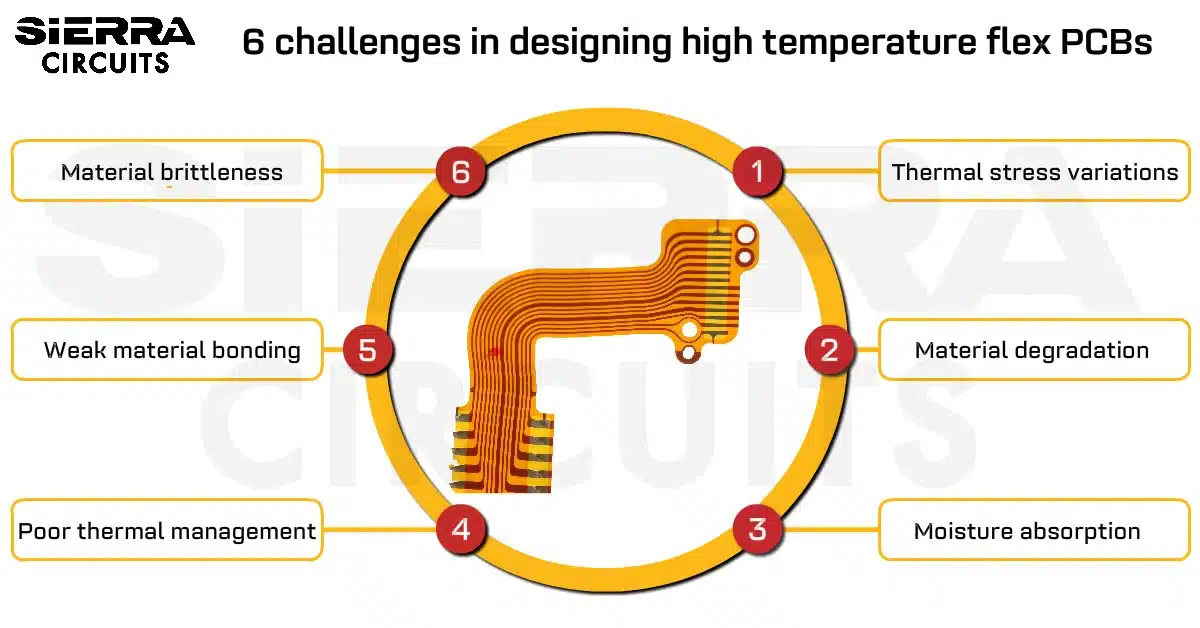
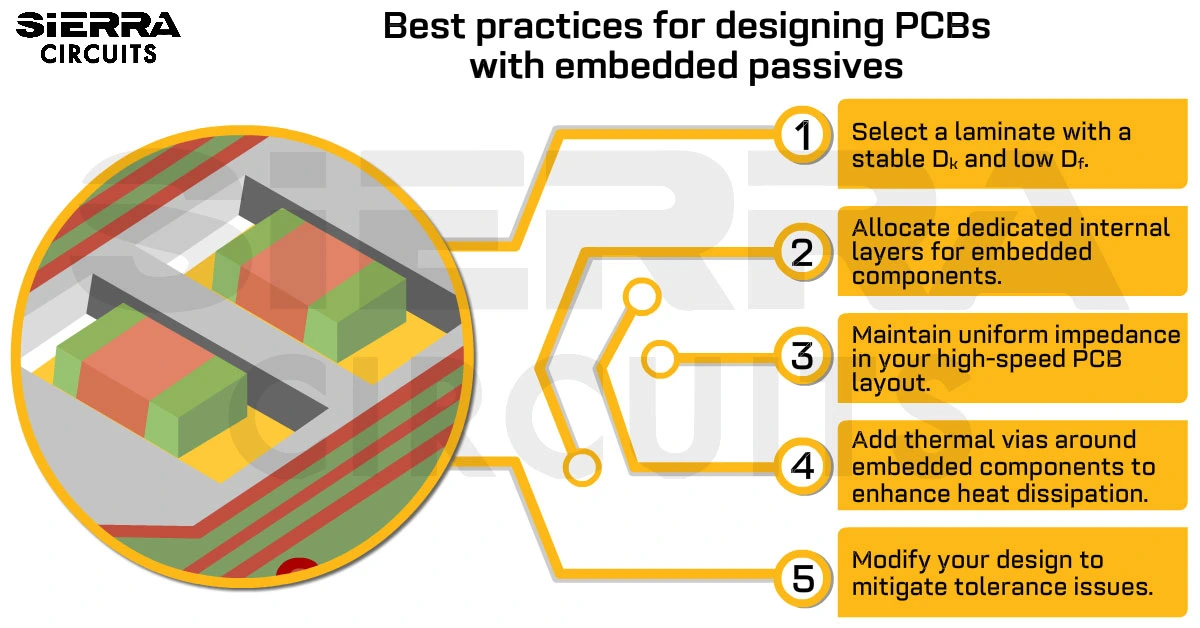
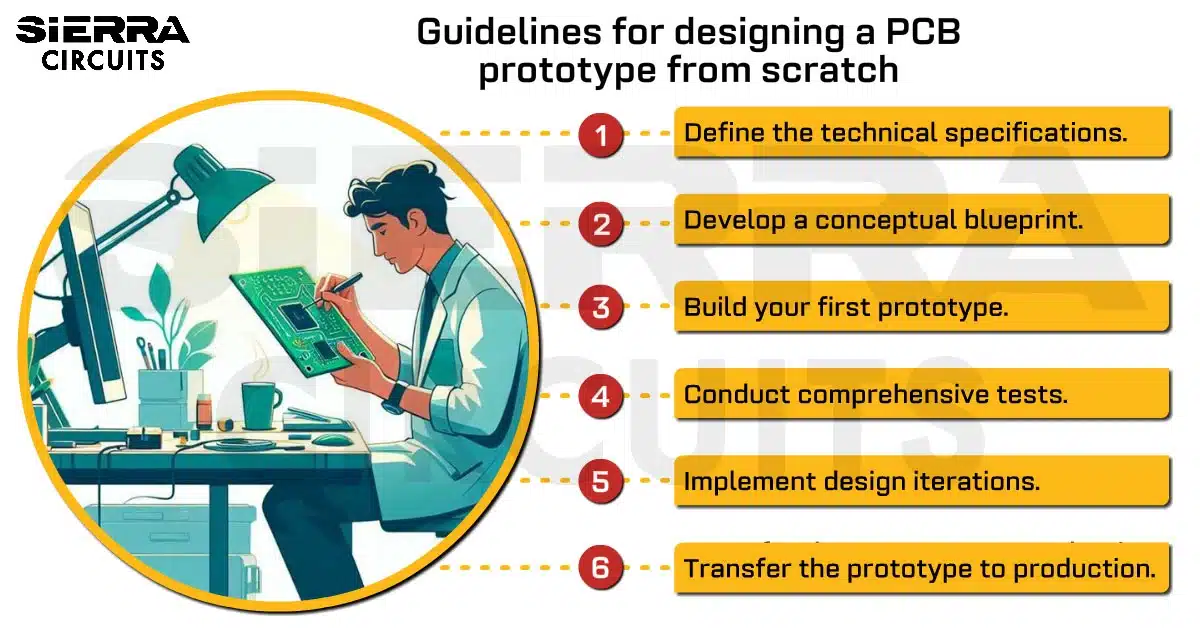
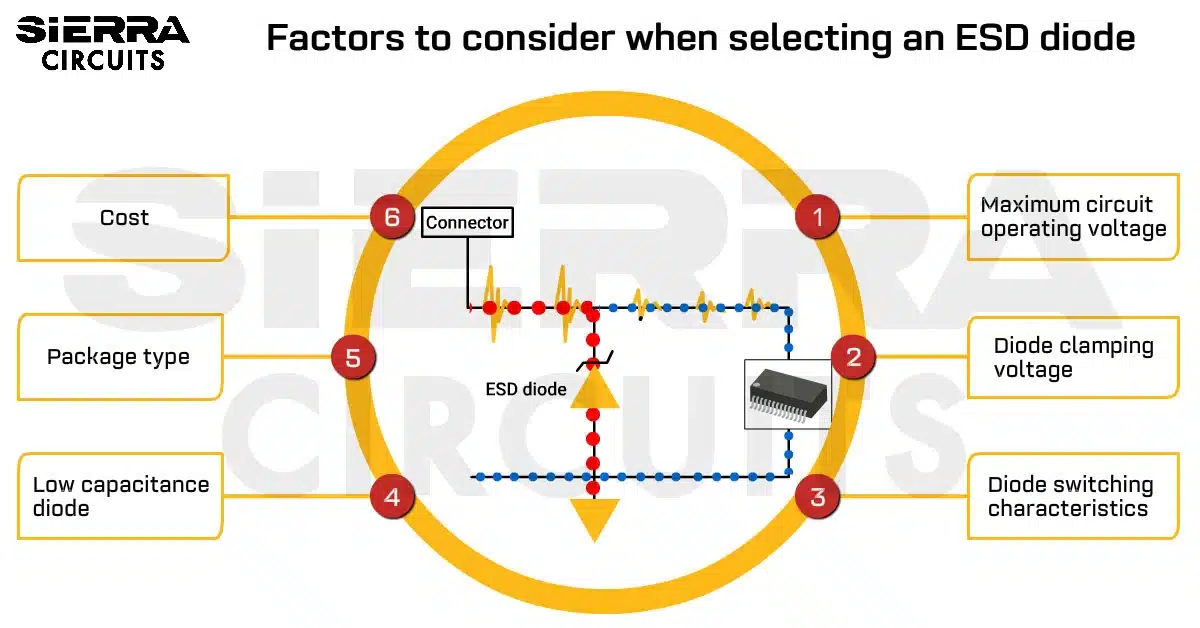
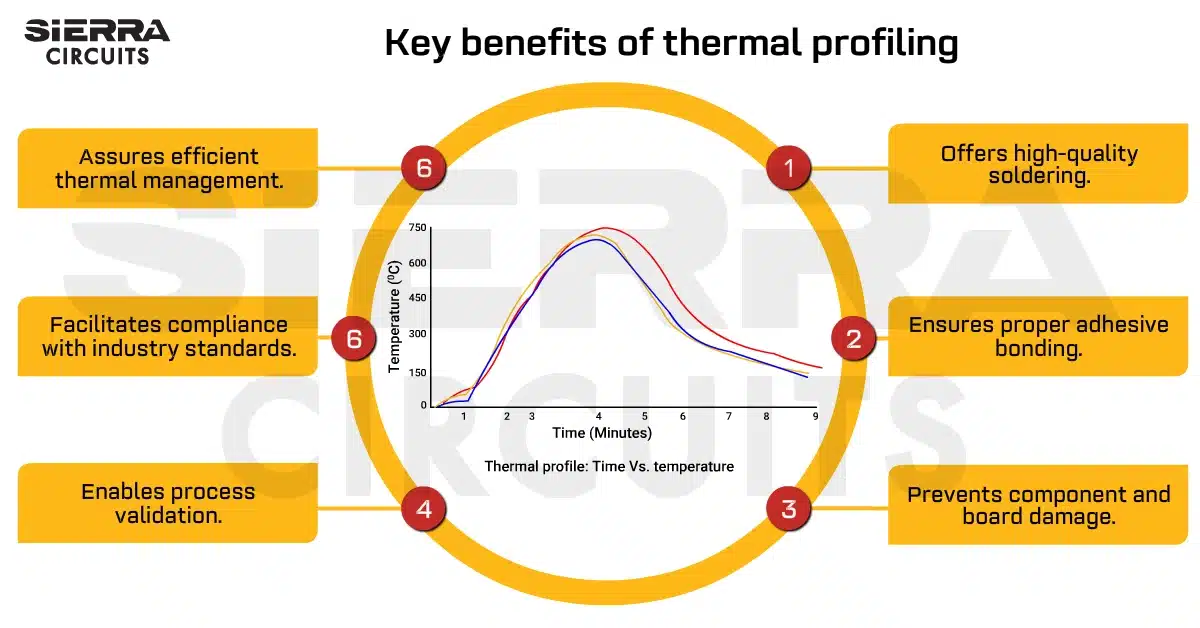
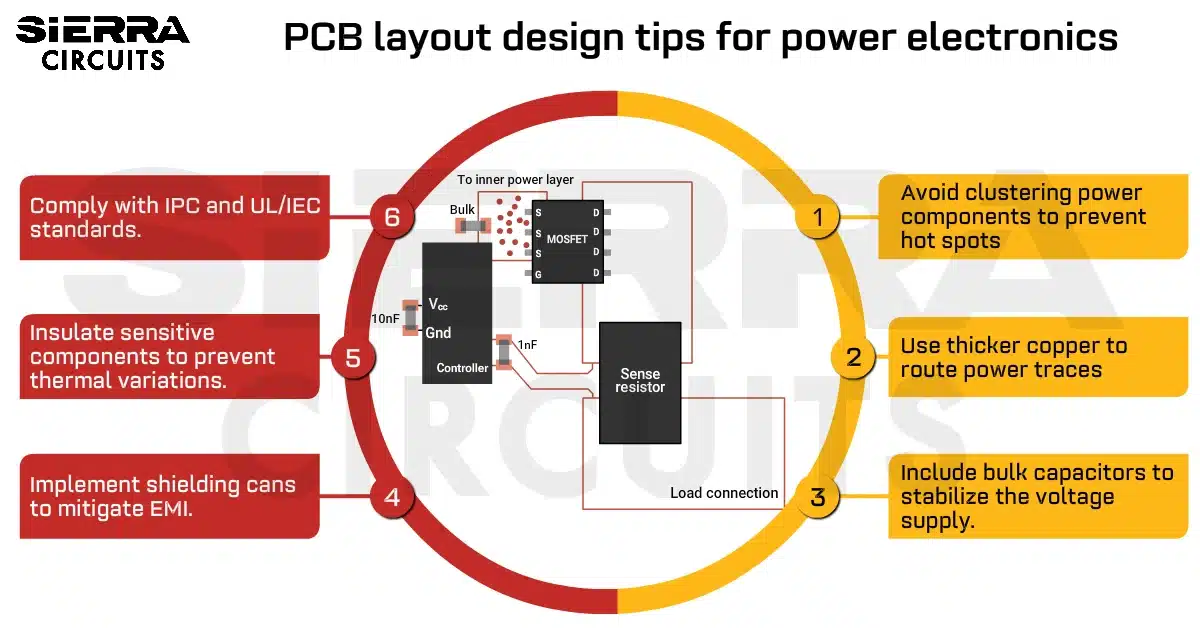
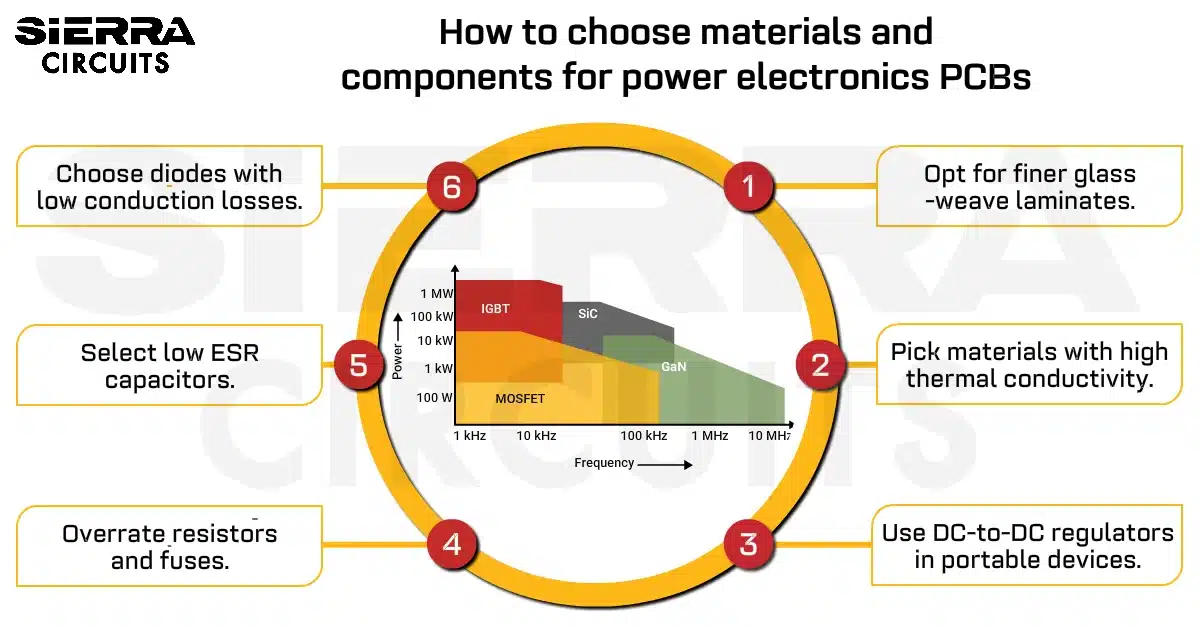
Design Guidelines

Download our design guides
for better PCB designing and manufacturing
These are some of the design guides designers and engineers download the most:
- DFM Handbook
- Controlled Impedance Design Guide
- HDI Design Guide
- PCB Transmission Line eBook
- High-Speed PCB Design Guide
- PCB Material Design Guide
- DFA Handbook

Fabrication, Procurement, & Assembly. PCBs fully assembled in as fast as 5 days.
- Bundled together in an entirely-online process
- Reviewed and tested by Engineers
- DFA & DFM Checks on every order
- Shipped from Silicon Valley in as fast as 5 days
Fabrication. Procurement & Assembly optional. Flexible and transparent for advanced creators.
- Rigid PCBs, built to IPC-6012 Class 2 Specs
- 2 mil (0.002″) trace / space
- DFM Checks on every order
- 24-hour turn-times available
Complex technology, with a dedicated CAM Engineer. Stack-up assistance included.
- Complex PCB requirements
- Mil-Spec & Class 3 with HDI Features
- Blind & Buried Vias
- Flex & Rigid-Flex boards